
The Bisection Method is a powerful algorithm that simplifies the process of locating roots within an interval.
It is based on the principle of repeatedly dividing an interval and narrowing down the search space until the root is found with a desired level of accuracy.
Bisection Method C++
The bisection method is an Algorithm or an Iterative Method for finding the roots of a Non-Linear equation.
The convergence in the bisection method is linear which is slow as compared to the other Iterative methods.
However, it is the simplest method and it never fails.
Also Read: Regula Falsi Method C++
Bisection Method C++ Program
//Biscection method c++
//techindetail.com
#include<iostream>
#include<math.h> //used for fabs() function.
#include<iomanip>//used for setw() and setprecision()
//they are used to just manipulate the output.
using namespace std;
//function definition
//it calculates the value of xsinx-1 for different values of x.
float f(float x)
{
return x*sin(x)-1;
}
//bisects the interval and counts the number of iterations
//by incrementing the value of itr.
void bisect(float *x,float a,float b,int*itr)
{
*x=(a+b)/2;
++(*itr);
cout<<"iteration no. "<<*itr<< " X = "<<setw(3)<< setprecision(5)<< *x<<endl;
}
int main()
{
int itr=0,maxitr;
float x,a,b,aerr,x1;
cout<<"Enter the values of a and b , allowed error, maximum iterations"<<endl;
cin>>a>>b>>aerr>>maxitr;
cout<<fixed;
bisect(&x,a,b,&itr);
do
{
if(f(a)*f(x)<0)
b=x;
else
a=x;
bisect(&x1,a,b,&itr);
if(fabs(x1-x)<aerr)//fabs() calculate the absolute value of (x1-x).
{
cout<<"After "<< itr <<" iterations, root"<< " = "<<setw(6)<< setprecision(4)<<x1<<endl;
return 0;
}
x=x1;
}while(itr<maxitr);
cout<<"Solution does not converege,"<<"iterations not sufficient"<<endl;
return 0;
}
Code language: PHP (php)In this code, we explore the implementation of the Bisection Method in C++ Program, highlighting its simplicity and effectiveness in solving equations.
Bisection Method Rule
This method is actually using Intermediate Value Property repeatedly.
If a function f(x) is continuous in a closed interval [a,b] and f(a) and f(b) have opposite sign.
Then The root lies between a and b and the first approximation of the root is x1=(a+b)/2.
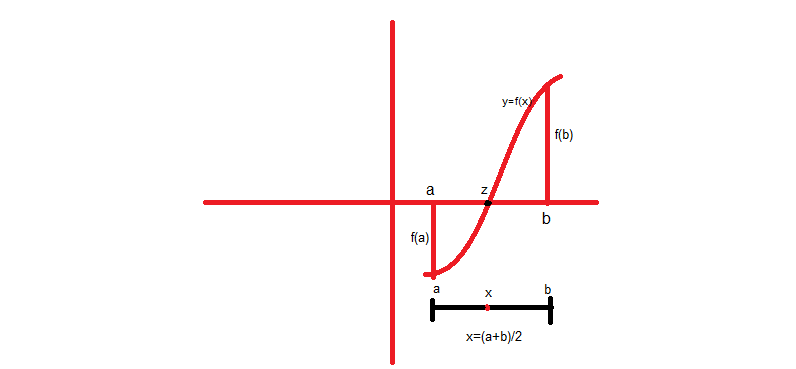
Related: Newton Raphson Method
Now the root lies between a and x1 or x1 and b accordingly if f(a) and f(x1) have an opposite sign or f(b) and f(x1) have opposite signs respectively.
Let the root lies between a and x1, then we again bisect the interval to find the next approximation of the root i.e. x2=(a+x1)/2, and continue the process until the root is found to the desired accuracy.
Related: Gauss Jordon Method C++

In the above figure, then f(x1) is positive and f(x0) is negative so the root lies between x1 and x0.
Then we bisect the interval and find x2 and f(x2) is also positive so the root lies between x0 and x2, and we find x3 and so on.
Also Read: Gauss Elimination Method C++
Bisection Method Example
Find the Root of the equation x3 – 4x – 9 = 0, using the bisection method correct to three decimal places.
Sol. Let f(x) = x3 – 4x – 9

Since every interval is half of its previous interval, i.e in each step the length of the interval is reduced by a factor of 1/2.
MCQ: The convergence in the bisection method is linear.
See Also: Partial Pivoting C++ Program
Suggested Read: Related Numerical Methods
