Circular Linked List in C++
Introduction:
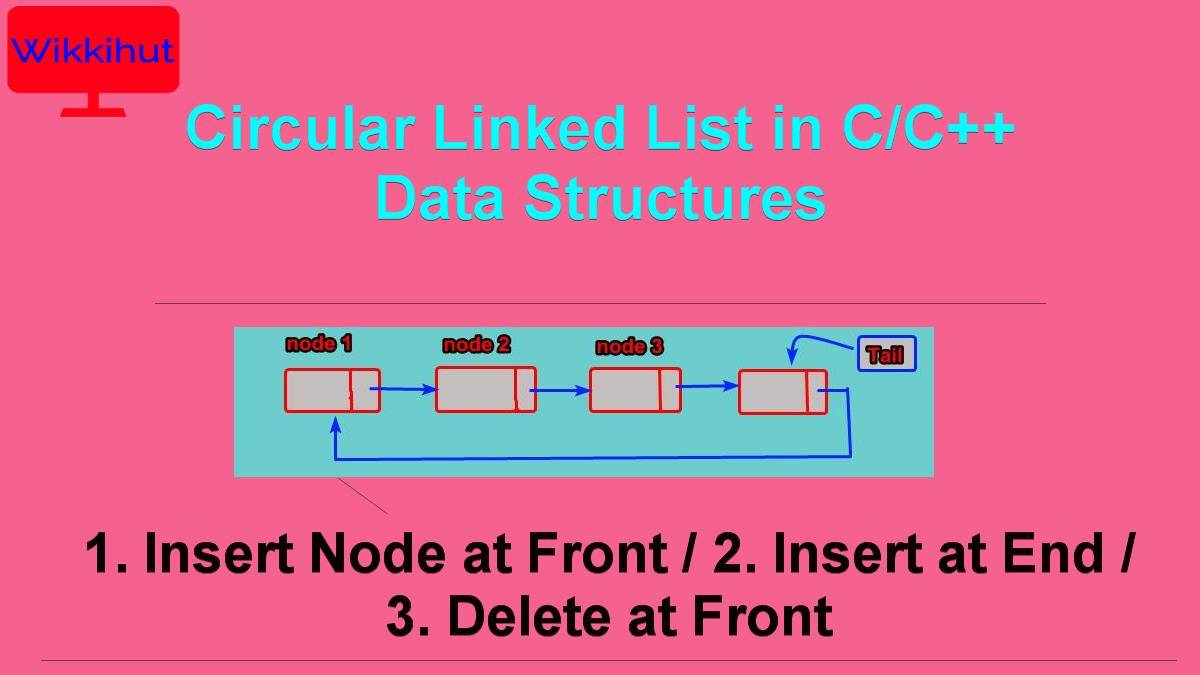
A Circular Linked list is simply a Linked List in which the link field of the last node contains the address of the first node of the list.
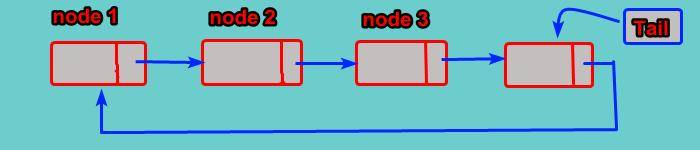
In the Circular Linked list, the link field of the last node does not point to NULL, rather it points back to the first node or head of the list, thus making it hypothetically circular in structure.
Also Read: Doubly Linked List C++
Therefore, it has no end so we must establish the First and Last nodes of this list, in order to access all the nodes. see more
For simplicity, we can assign only the Tail pointer to access the whole list because the last node or tail is not set to null it points to the first node, so we access the first node just like Tail->next is head done.
Must Read: Stack Using Array In C++
Circular linked list C++ Program
//Circular Linked Lists c++
//techindetail.com
#include<iostream>
using namespace std;
struct Node
{
int data;
Node *next;
}*tail;
class Circular_LinkedList
{
public:
void Insert_at_Front(int n);
void Insert_at_End(int n);
void Delete_at_Front();
void Display();
};
int main()
{
int choice;
Circular_LinkedList object;
tail=NULL;
while(1)
{
cout<<"\n\t Press 1 for Insert at Front\n";
cout<<"\t Press 2 for Insert at End\n";
cout<<"\t Press 3 for Delete at Front\n";
cout<<"\t Press 4 for Display Nodes\n";
cout<<"\t Press 5 to Exit\n";
cout<<" Enter you Choice: \n";
cin>>choice;
switch(choice)
{
case 1:
object.Insert_at_Front(3);//Passing values
object.Insert_at_Front(2);
object.Insert_at_Front(1);
break;
case 2:
object.Insert_at_End(4);
object.Insert_at_End(5);
break;
case 3:
object.Delete_at_Front();
break;
case 4:
object.Display();
break;
case 5:
exit(0);
default:
cout<<"Wrong Choice\n";
}
}
return 0;
}
void Circular_LinkedList::Insert_at_Front(int n)
{
Node *temp;
temp=new Node;
temp->data=n;
temp->next=NULL;
if(tail==NULL)
{
tail=temp;
tail->next=tail;
}
else
{
temp->next=tail->next;
tail->next=temp;
}
}
void Circular_LinkedList::Insert_at_End(int n)
{
Node *temp;
temp=new Node;
temp->data=n;
temp->next=NULL;
if(tail==NULL)
{
temp->next=temp;
tail=temp;
}
else
{
temp->next=tail->next;
tail->next=temp;
tail=temp;
}
}
void Circular_LinkedList::Display()
{
Node *front;
front=tail->next;
if(tail==NULL)
{
cout<<"Empty List: \n";
}
cout<<"\tNodes are:\t";
while(front!=tail)
{
cout<<front->data<<" --> ";
front=front->next;
}
if(front==tail)
{
cout<<front->data;
}
delete front;
cout<<endl;
}
void Circular_LinkedList::Delete_at_Front()
{
Node *temp=new Node;
temp=tail->next;
if(tail==NULL)
{
cout<<"Empty List\n";
return;
}
if(temp==tail)
{
delete temp;
}
else
{
tail->next=temp->next;
delete temp;
}
}Code language: PHP (php)Related: Doubly Circular Linked List C++
Why circular linked list C++?
- The Nodes are accessed easily because we can traverse the list from the tail to back to the list.
- And the Deletion is also easy, by traversing from head to tail and from tail to head back.
- It is Best for Searching and Sorting Algorithms because it is time-sufficient.
Suggested: Queue Using Array in C++
Operations on Circular Linked List.
All the operations that are possible for the simple linked list are also applicable to the circular linked lists.
We can use operations Like, Insert at the end, insert at front, insert in between, delete front, delete at the end, delete at the middle, etc.
- Insertion
- Deletion
- Traverse
1. Insertion Algorithm
a. Insert at End:
First Create a new node like Node *temp=new node and assign data temp->data=n, temp->next=NULL;
1. If(Tail==NULL); Now if it is the first node then,
a. put temp->next=temp like temp is pointing to temp thus making it circular because the last node of the list is pointing to the first node.
b. After assigning put temp in the tail like Tail=temp, because there is only one node so it is tail.
2. Else, if there are nodes inserted already, the tail is not now null.
a. Temp->Next=Tail->Next; Recall we are inserting at the end, so temp is going to end, and what ends points it points the first node, tail->next is the first node.
b. Tail->Next=Temp; what tail is for it points the last now the temp is going the last node, so the tail is now temp.
c. Tail=Temp; Now temp is the new tail in the list.
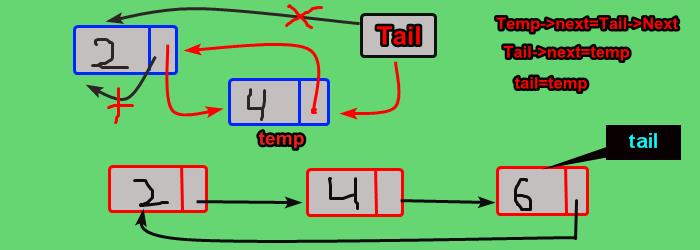
b. Insert at Front or Add at Begin:
First, create a new node temp with data n and link with NULL the same as above.
- If(tail==NULL), that means there is no node.
- so tail=temp, tail->next=tail.
- Else, there are some nodes either 1, 2 or much more.
2. Temp->Next=Tail->Next; Now look here tail-next is actually the first node, so we are pointing head to the new node.
because we are inserting at the front, thus temp is going to be the first node.
3. Tail->Next=Temp; Now the tail is pointing to the temp making it a new head.
Must Read: Types of Binary Trees C++
3. Display();
Now display or traverse in a circular linked list is different from the simple linked list because in this list we must terminate it otherwise it will go in an infinite loop.
- Make a temporary pointer Node *front and assign it to the first node like front=tail->next.
- First check if(tail==NULL) then cout empty list;
- start a while loop While(front!=tail) that means traverse till tail is visited.
- Inside loop display the data like cout<
data; Now all nodes are visited except the tail, now outside the loop set condition if(front=tail) then simply display it and all the nodes are now printed.
2. Deletion Algorithm
Delete at Front
- Create a node pointer *temp;
- Check if the list is empty like If(tail==NULL) then simply print cout<<“List Empty”; and Return;
- Also if there is only one node, if(tail==tail->next) then set tail==Null.
- Else, Since we are deleting the head, so first put the head in temp as temp=tail->next;
- now we need to assign new head node to tail, i.e, tail->next=temp->next
- Delete temp and Return now all is done;