Binary Search Tree | BST Operations Insertion, Deletion, Search

What Is Binary Search Tree

A binary Search tree is a special type of Binary Tree, in which all the nodes are arranged in a specific order.

The binary search tree is either empty or satisfies the following properties:

• The value of the left child or the left sub-tree is always less than the value of the root.
• Similarly, value of all the nodes in the right sub-tree is always greater than to the value of root node or equal to the value of the root.
• This rule is applicable to all the left and right sub trees of the root recursively.

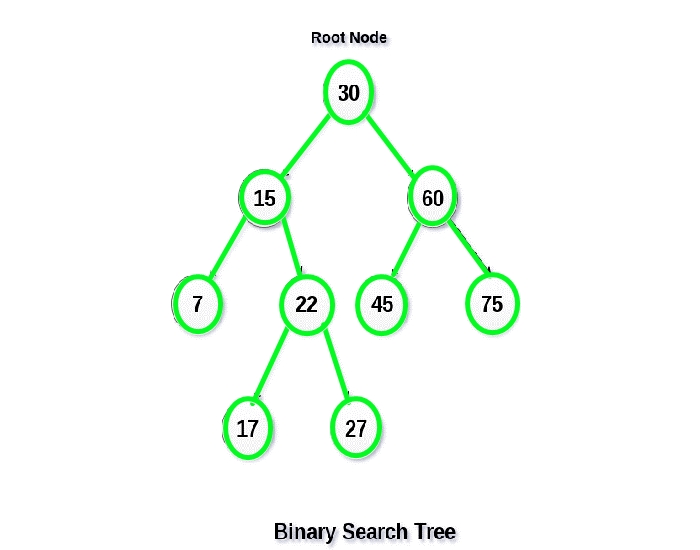
Each node contains a key, a value, a left link, a right link, and a node count. The left link points to a BST for items with smaller keys, and the right link points to a BST for items with larger keys.

A binary search tree is also called an Ordered Binary Tree.

Time Complexity BST

1. Search O(n)
2. Insertion O(1)
3. Deletion O(n)

The Time Complexity of a Binary Search Tree for searching any element is O(log₂n).

And the time complexity in the worst case, to search an element is O(n).

Recursive Search

If the tree is empty, we have a search miss; if the search key is equal to the key at the root, we have a search hit. Otherwise, we search recursively in the appropriate subtree until the particular node is found.

BST Example

Example 1

Create the binary search tree using the following data elements. 43, 10, 79, 90, 12, 54, 11, 9, 50?

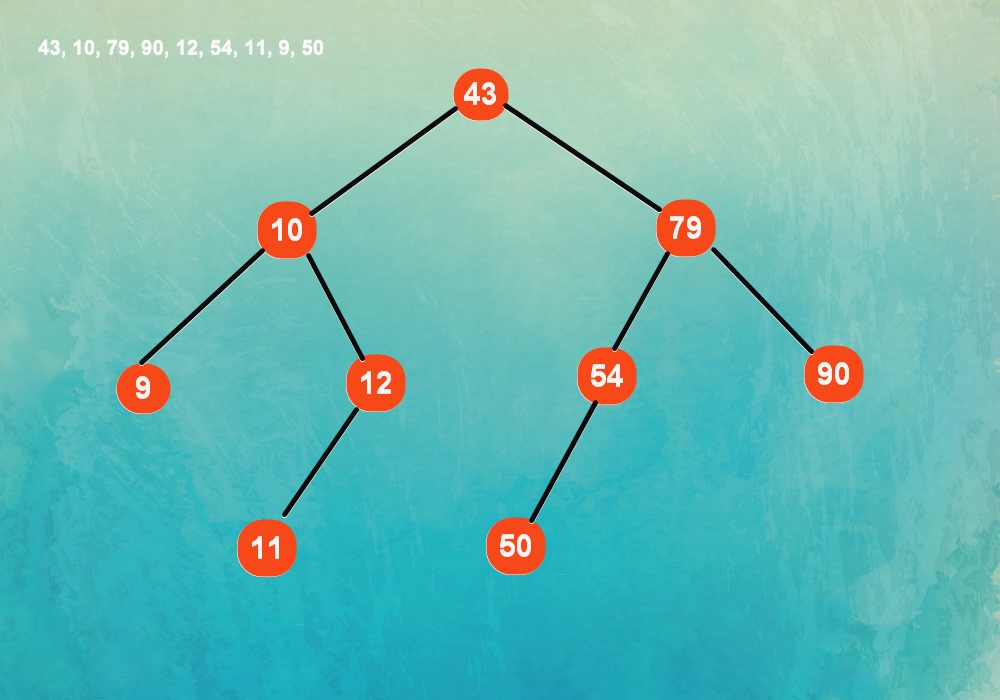
1. Insert 43 as the root of the tree.
2. 10 is less than 43, insert it into left.
3. 79 is bigger than 43, insert it into right.
4. Repeat steps.

Example 2

Construct a Binary Search Tree by inserting the following sequence of numbers. 10, 12, 5, 4,20,8,7,15 and 13?

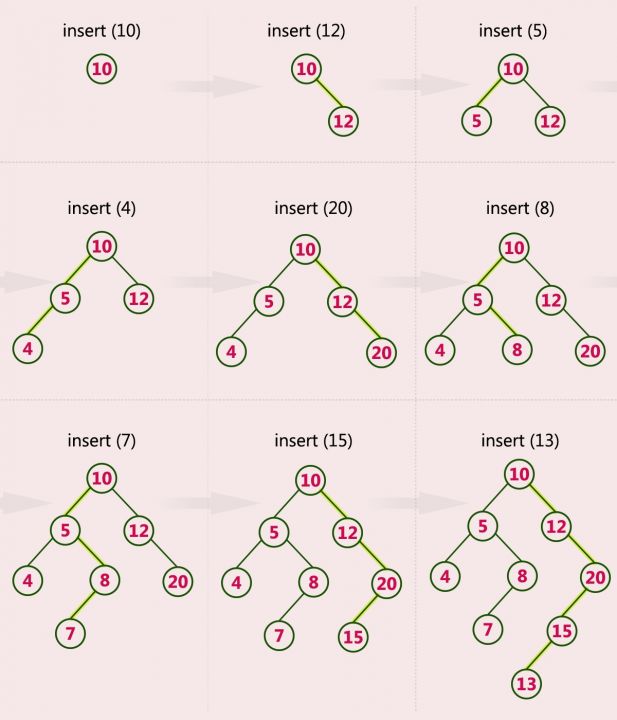
1. Insert 10 a root node.
2. Insert 12 to right node.
3. Insert 5 to left.
4. Insert 4 to the left of 5.
5. Repeat.

Operations on Binary Search Tree (BST)

The following operations are performed on a binary search tree…

• Search
• Insertion
• Deletion

Search Operation in BST

In a binary search tree, the time complexity of the Search operation is O(log n.

The search operation is performed as follows.

• Step 1 – Read the search element from the user.
• Step 2 – Compare this with the value of root node.
• Step 3 – If given value is equal to root, display and exit.
• Step 4 – If not equal, then check whether search element is smaller or larger than that node value.
• Step 5 – If search element is smaller, then continue the search process in left subtree.
• Step 6- If search element is larger, then continue the search process in right subtree.
• Step 7 – Repeat the same until we find the exact element or until the search element is compared with the leaf node
• Step 8 – If found then display “Element is found” and terminate the function.
• Step 9 – If not found, then display “Element is not found” and exit.

Insertion Operation in BST

Insertion operation in BST is not much more difficult to implement than search. Indeed, a search for a key not in the tree ends at a null link, and we need to do is replace that link with a new node containing the key.

The Time Complexity of Insertion Operation in the Binary Search Tree is O(log n).

In a binary search tree, a new node is always inserted as a leaf node.

The insertion operation is performed as follows…

1. Create a new Node containing data.
2. Set its left and right link to NULL.
3. Check whether tree is Empty.
4. If the tree is Empty, then set root to newNode.
5. If the tree is Not Empty, then check whether the value of newNode is smaller or larger than the node.
6. If newNode is smaller  then move to its left child.
7. If newNode is larger then move to its right child.
8. If new node is equal to the root, move to right child.
9. Repeat the above steps until we reach to the leaf node

Deletion Operation in BST

The Time Complexity of Deletion operation in BST is O(log n).

The Deletion operation in the binary search tree is difficult than insertion. Deletion is easy only if the tree has only one child (or no children).

But what can we do to delete a node that has two children? We are left with two links but have a place in the parent node for only one of them.

The Solution is to delete a node x by replacing it with its successor. Because x has a right child, its successor is the node with the smallest key in its right subtree. The replacement preserves order in the tree because there are no keys.

BST Deletion has the following three cases.

• Deleting a node with no children
• Deleting a node with one child
• Deleting a node with two children

Case 1: Deleting a leaf node

Use the following steps to delete a leaf node from BST…

• Find the node to be deleted using search operation
• Delete the node using free function and terminate the function.

Case 2: Deleting a node with one child

Use the following steps to delete a node with one child from BST…

• Find the node to be deleted using search operation
• If it has only one child then create a link between its parent node and child node.
• Delete the node using free function and terminate the function.

Case 3: Deleting a node with two children

We use the following steps to delete a node with two children from BST…

• Find the node to be deleted using search operation
• If it has two children, then find the largest node in its left subtree, Or the smallest node in its right subtree.
• Swap both deleting node and node which is found in the above step.
• Then check whether deleting node came to case 1 or case 2 or else goto step 2
• If it comes to case 1, then delete using case 1 logic.
• If it comes to case 2, then delete using case 2 logic.
• Repeat the same process until the node is deleted from the tree.

Advantages of binary search tree

1. Efficient Searching
2. Time Complexity O(log2n)
3. Time Complexity Worst Case O(n)
4. Fast Insertion
5. Fast Deletion

In Binary Search Tree, Searching a particular element is very easy, as compared to arrays, and linked lists.

In the searching process, it removes half the sub-tree at every step and thus reduces the total time of traversal.

It also speeds up the insertion and deletion operations as compared to that in the Array and Linked list.