
Newton Forward Difference Interpolation C++
Newton’s forward difference interpolation is used when the function is tabulated at equal intervals.
If the data point to be interpolated lies in the upper half or in the beginning of the table then Newton’s forward difference interpolation is used because it gives the better approximation.
In order to interpolate at any point (say x) between X0 and Xn, Newton’s forward interpolation formula takes the form.
Also Read: Lagrange’s Interpolation Formula
Formula
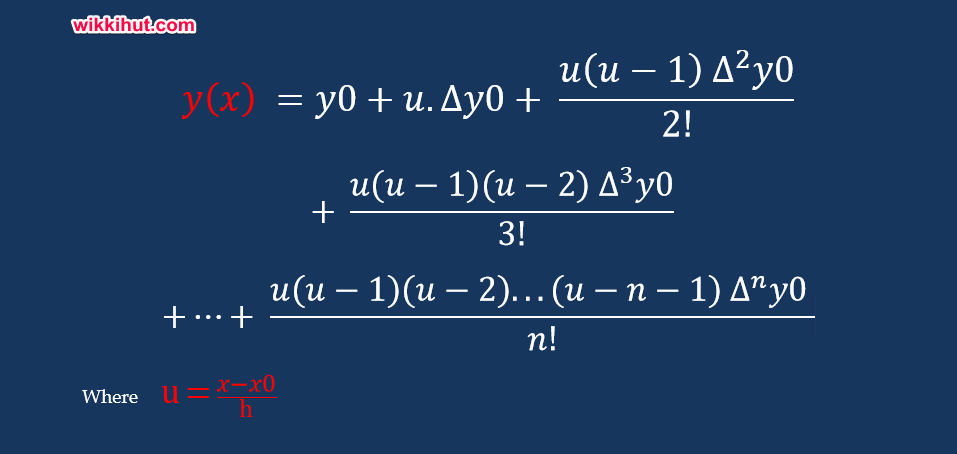
Where,
U = ( x- x0 ) / h
‘h’ is the interval between data points
’∆‘ is the forward difference symbol
Must Read: Bisection Method C++ Program | Example
C++ Program
Newton Forward Difference Interpolation C++ Program
//Newton's Forward Difference interpolation
//techindetail.com
#include<iostream>
#include<bits/stdc++.h>
//for specifying format
using namespace std;
int factorial(int n){
int fact=1;
while(n){
fact=fact*n;
n--;
}
return fact;
}
int main(){
float x[10],y[10],p[10],diff[10];
float X,f,f2=0,u,h;
int i, j=1,n,k=1;
cout<<"Enter the number of observations: ";
cin>>n;
cout<<"\nEnter the values of xi's and f(xi's)\n";
for(i=1; i<=n; i++){
cout<<"x["<<i<<"]: ";
cin>>x[i];
cout<<"f["<<i<<"]: ";
cin>>y[i];
}
cout<<"\nx[i's]\tf[i's]\n";
for(i=1; i<=n; i++){
cout<<x[i]<<"\t"<<y[i]<<"\n";
}
cout<<"\nEnter the value of x at which
// you want to interpolate: ";
cin>>X;
int m=n;
h=x[2]-x[1];
u=(X-x[1])/h;
//saving (y[1]) because the array y[] changes
// and we have add it at the last result
f=y[1];
cout<<fixed<<setprecision(2);
cout<<"Forward Difference table for the given set of points is\n";
do{
cout<<"diff.("<<j++<<") f(x)\n";
for(i=1; i<n; i++){
p[i]=( ( y[i+1]-y[i] ) );
cout<<p[i]<<"\n";
//this assignment is done because we are computing the new
//difference array using previous one (delta f(x)'s)
y[i]=p[i];
}
diff[k++]=p[1];
n--;
cout<<"\n";
}while(n!=1);
float df=u;
float l=1;
for(int i=1; i<m; i++ ){
if(i>1)
df=df/factorial(i);
f2=f2+(df*diff[i]);
for(int j=0; j<=i; j++){
l=l*(u-j);
}
df=l;
}
f=f+f2;
cout<<"\nf("<<X<<") = "<<f;
return 0;
}
Code language: C++ (cpp)Also Read: Maclaurin Series Formula | Example
Formation of Forward Difference table
Before studying Newton’s Forward Difference interpolation, we should know how to form a forward difference table. Therefore, first, we will see how to form a forward difference table.
General Example
Consider the following general set of data points.
| X | x0 | x1 | x2 | x3 | x4 | x5 |
| Y | y0 | y1 | y2 | y3 | y4 | y5 |
The forward difference table for the above set of data points is given below:

Suggestion: Gauss Jordan Method C++ Program | Example
Example
Newton Forward Difference Interpolation C++ Example:
Q. Consider the following set of data points and form a forward difference table.
| X | 2.0 | 2.25 | 2.50 | 2.75 | 3.0 |
| Y | 9.0 | 10.06 | 11.25 | 12.56 | 14.0 |
Find y (2.35)?
Ans. The forward difference table for the given set of data points is given below:
Ans. We have,
x = 2.35, ( given )
h = x1 – x0 = 2.25 – 2.0 = 0.25
u = (x-x0) / h = (2.35-2.0)/0.25 = 0.35/0.25 = 1.4
Now, the forward difference table is as:

Now you can calculate y( x )
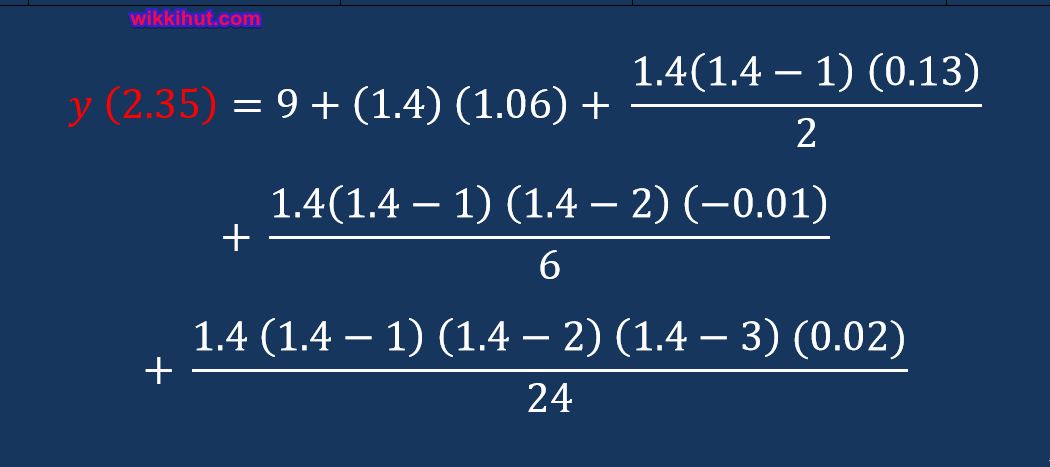
y (2.35) = 10.484 + 0.0364 + 0.00056 + 0.000448
y(2.35) = 10.52141
Related: Numerical Techniques Using C++
Suggested Read:
