Regula Falsi Method with C++ Program

Table of contents

Regula Falsi Method

Method of False Position

The Regula-Falsi method is also called the Method of False Position, closely resembles the Bisection method. This is the oldest method of finding the real root of an equation.

Regula falsi method has linear rate of convergence which is faster than the bisection method.

Related: Newton Raphson Method C++

Regula Falsi Method C++ Program

//Regula Falsi method
   //techindetail.com

#include<iostream>
#include<math.h>
#include<iomanip>
using namespace std;

float f(float x)
{
	return cos(x)-x*exp(x);
}
void regula (float *x, float x0,float x1, float fx0,float fx1, int *itr)
{
	*x=x0-((x1-x0)/(fx1-fx0))*fx0;
	++(*itr);
cout<<" Iteration No."<<setw(3)<<*itr<<"\t X= "<<setw(7)<<setprecision(5)<<*x<<endl;

}
int main()
{
	int itr=0, maxitr;
	float x0,x1,x2,x3,aerr;
	cout<<"\nEnter the value of x0: ";
	cin>>x0;
	cout<<"\nEnter the value of x1: ";
	cin>>x1;
	cout<<"\n enter allowed error: ";
	cin>>aerr;
	cout<<"\n maximum iterations: ";
	cin>>maxitr;
	cout<<endl;
	regula(&x2,x0,x1,f(x0),f(x1),&itr);
	do
	{
		if(f(x0)*f(x2)<0)
		x1=x2;
		else
		x0=x2;
		regula(&x3,x0,x1,f(x0),f(x1),&itr);
		if(fabs(x3-x2)<aerr)
		{
		cout<<"After "<<itr<<" iterations, root = "<<x3<<endl;
		return 0;
		}
		x2=x3;
	}
  while(itr<maxitr);

    cout<<"Solution does not converge"<<endl;
	cout<<"Iterations are not sufficient"<<endl;
	return 1;

}Code language: C++ (cpp)

Read More: Gauss Jordan Method C++

Example

Find a real Root of equation f(x)=x³-2x-5 by the method of false position method ( Regula Falsi method ).

let f(x)=x³-2x-5 and we have to find its real root correct to three decimal places.

if we put x=2 and x=3, we find f(2) is negative and f(3) is positive.
it means the root lies between 2 and 3.

therefore, taking
x₀ = 2
x₁ = 3
f ( x₀ ) = -1 and
f ( x₁) = 16
in equation (2) we get
x₂ = 0.0588

Now f(x₂) = f( 0.0588 ) = -0.3982

i.e., the root lies between 2.0588 and 3.

Therefore, taking

x₀ = 2.0588

x₁ = 3

f ( x₀) = -0.3908

f ( x₁) = 16 in eq. (2)

we get, x₃ = 2.0813

By repeating this process, the successive approximations are

x₄=2.0682 x₅=2.0915
.
.
.
x₇=2.0941 and
x₈=2.0943
and therefore the root is 2.094

Gauss elimination Method C++

Suggested Read:

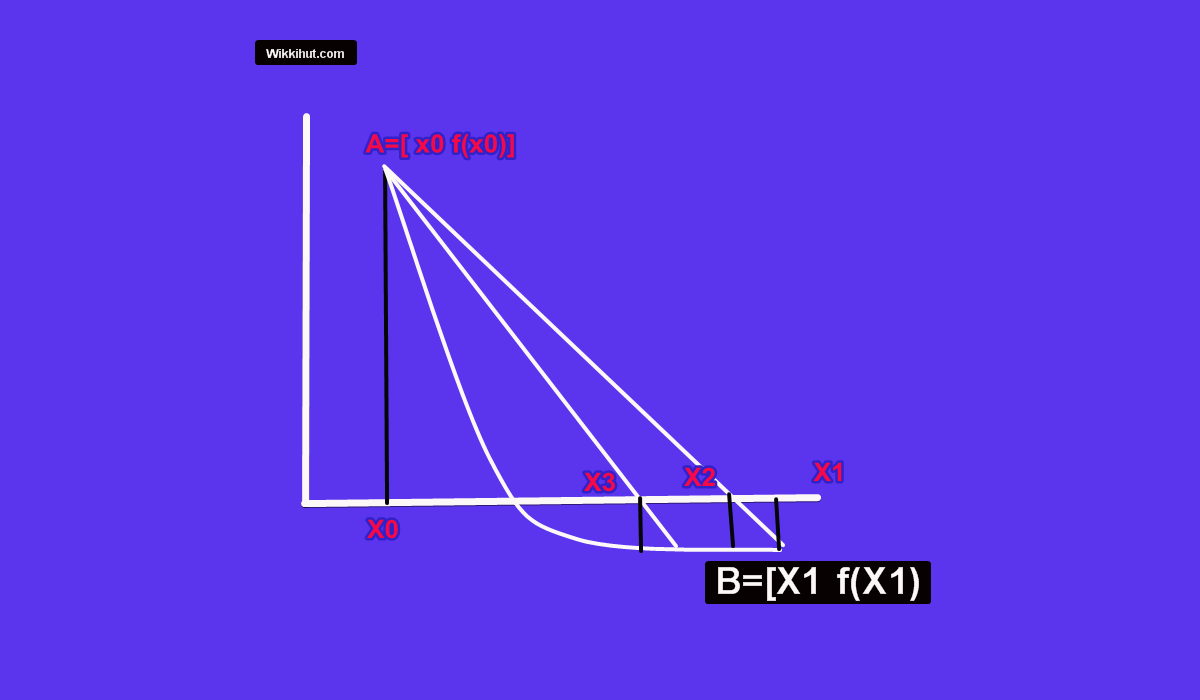
Graphical explanation.

As in the picture we use two points x0 and x1 such that f(x0) and f(x1) have opposite signs, that is the graph
y=f(x)
cuts the x-axis at least once while going from x₀ to x₁, which indicates that the root lies between x₀ and x₁ .

Now we connect the two points f(x₀) and f(x₁) by a straight line.

The equation of the straight line joining these points is :

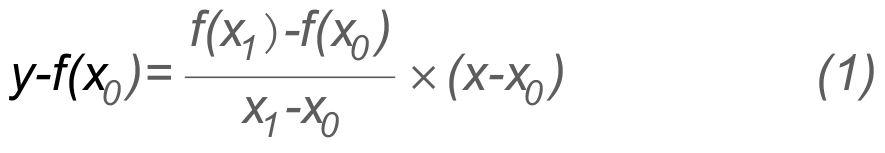
This straight-line cuts the x-axis at point x2,
this point where the line (1) cuts the x-axis is taken as an approximation to the root.

At this point Y=0 and X=x₂ put the value of Y and X in (1) we get:

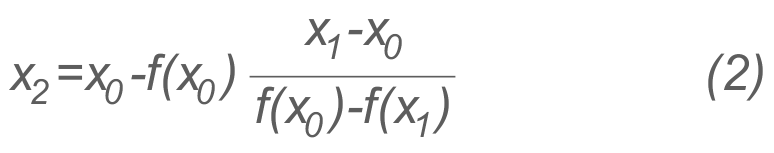
which is an approximation to the root. see more

Find f(x₂).
If f(x₂) and f(x₀) are of opposite signs then we replace x₁ by x₂ and draw a straight line connecting
f(x₂) to f(x₀)
to find the new intersection point.

If f(x2) and f(x0) are of the same sign then x0 is replaced by x2 and proceed as before.
In both cases, the new interval of search is smaller than the initial interval and ultimately convergence is guaranteed.

Read More: Gauss elimination with Partial Pivoting C++

Algorithm for Regula-falsi method:

read x0 & x1, two initial guesses.
Enter Allowed error and Max iterations.
Take x0=1 & x1=3
f(x0)=-0.3908 and f(x1)=16, in equation (2) we get x3=2.0813
(x0) and f(x1) are not same.
f0=f(x0)
f1=f(x1)
for i=1 to n in steps of 1 do
x2=(x0f1-x1f0)/(f1-f0)
f2=f(x2)
if |f2|<e then
begin Write ‘convergent solution’, x2,f2
stop end
if sign (f2)=sign f(0)
then begin x0=x2
f0=f2
else begin x1=x2
f1=f2
write ‘Does not converge in n iterations’
write x3,f2
stop