Newton-Raphson Method C++ Program / Example Formula

Newton’s Method

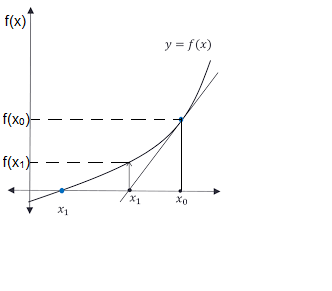
Intro:- Newton-Raphson method also called as Newton’s Method is used to find simple real roots of a polynomial equation.

It has the fastest rate of convergence. The method is quite sensitive to the starting value.

It may also diverge if the first derivative i.e.f'(x) of the function is near zero during the iterative cycle. see more

C++ Program Newton Raphson Method

//Newton raphson method c++ 
//techindetail.com

#include<iostream.h>
#include<math.h>
float fun(float x)//we are finding the root of x^4-x-10
{
   return x*x*x*x-x-10;
}
float diff(float x) differential of x^4-x-10;
{
return 4*x*x*x-1;
}
int main()
{
  int itr,maxitr;
  float h,x0,x1,aerr;
  cout<<"Enter x0,allowed error, maximum iterations"<<endl;
  cin>>x0>>aerr>>maxitr;
  for(itr=1;itr<=maxitr;itr++)
{
  h=fun(x0)/diff(x0);
  x1=x0-h;
  if(fabs(h)<aerr)
    {
      cout<<"after "<<itr<<" root = "<<x1<<endl;
      return 0;
    }
  x0=x1;
}
  cout<<"Iterations not sufficient, Solution does not converge"<<endl;
return 1;
}Code language: C++ (cpp)

Algorithm for Newton Raphson method c/c++:

1.  Read  x0, e, n, N where x0 is the initial guess of the root, e the allowed error, n the order of the polynomial, and N the total number of iterations.
2. for i=0 to n in steps of 1 do Read bi end for.
3. for i=0 to n-1 in steps of 1 do Read bi end for.
4. P=an
5. bn-1=an
6. S=bn-1
7. for k=1 to N in steps of 1 do
8.    for i=1 to n-1 in steps of 1 do
9. b_n-(i+1)=a_n-i+x0b_n-i
10. S=b_n-(i+1)+x0S
    endfor
11. P=a0 + b0x0
12. x1=x0-(P/S)
13. if |x1–x0/x1| ≤ e goto step 18
    else
14. x0=x1
    endif
    endfor
15. write “root not found in N iterations”
16. write S, P, x1, x0
17. stop
18. write “root found in k iterations”
19. x0=x1
20. write  x0, S, P
21. stop

Some observations about Newton Raphson method c:

1. Newton’s method is useful in cases of large values of f'(x) e.e.
2. when the graph of f(x) while crossing the x-axis in nearly vertical.
      For if f'(x) is small in the vicinity of the root, then by h=-f(x)/f'(x),   
3.  h will be large and the computation of the root is slow or may not be possible.
4. Thus this method is not suitable in those cases where the graph of f(x) is nearly horizontal while crossing the x-axis.
5. Newton’s method is applicable to both algebraic and transcendental equations.
6. Newton’s method is useful when x0 is chosen sufficiently close to the root.
7. Newton’s Method has second-order convergence.