Gauss Elimination Method C++ Program Algorithm & Example

Gaussian Elimination Method in C++: A Quick and Efficient Solution for Linear Equations

Looking for a fast and efficient way to solve systems of linear equations?

Our blog post explores the Gaussian elimination method implemented in C++, providing you with a streamlined solution for your numerical analysis needs.

Gauss Elimination Method C++

Gauss Elimination Method is a direct method to solve the system of linear equations.

It is quite general and well-adaptive to computer operations and Numerical Techniques.

Gauss Elimination Method gives us the exact value of variables.

Simultaneous linear equations occur quite often in computational processes in almost every field.

• In engineering and science.
• Economics and Statistics
• Analysis of Electronic Circuits
• Output and Cost in Chemical Plants
• Optimizing Techniques
• Graphical methods and illustrations
• Numerical Techniques

Must Read: Lu Decomposition Method C++

So the solutions to these problems can be found through Direct and Iterative Methods.

Also Read: Partial Pivoting C++ Program

Gauss Elimination Method C++ Program

//Gauss Elimination Method C++ code
//techindetail.com

#include<iostream>
#include<iomanip>
#include<cmath>
#define N 3
	using namespace std;

int main()
{
	float Matrix[N][N+1],x[N];
		// Matrix = Augumented Matrix [Ad]
	float temp,s;

	//variables for loops
	int i,j,k;

	//Scan values of Matrix.

	cout<<"Enter Elements of "<<N<<" Rows & "<<N+1<<" Columns\n";
	cout<<fixed;

	for(i=0; i<N; i++)
	{
		cout<<"\tEnter Row  "<<i+1<<" & Press Enter\n";
		for(j=0; j<N+1; j++)
		cin>>Matrix[i][j];
	}

	 //make above matrix upper triangular Matrix

	for(j=0; j<N-1; j++)
	{
		for(i=j+1; i<N; i++)
		{
			temp=Matrix[i][j]/Matrix[j][j];

			for(k=0; k<N+1; k++)
				Matrix[i][k]-=Matrix[j][k]*temp;
		}
	}
	
		//print the Upper Triangular matrix

	cout<<"\n ---------------------------------\n";
	cout<<"\n Upper Triangular Matrix is:\n";
	for(i=0; i<N; i++)
	{
		for(j=0; j<N+1; j++)
		cout<<setw(8)<<setprecision(4)<<Matrix[i][j];
		cout<<endl;
	}
	
	//find values of x,y,z using back substitution

	cout<<"\n ---------------------------------\n";

	for(i=N-1; i>=0; i--)
	{
		s=0;
		for(j=i+1; j<N; j++)
		s += Matrix[i][j]*x[j];
		x[i]=(Matrix[i][N]-s)/Matrix[i][i];
	}

	//print values of x,y,z

	cout<<"\n The Solution is:\n";
	for(i=0; i<N; i++)
	 cout<<"x["<<setw(3)<<i+1<<"]="<<setw(7)<<setprecision(4)<<x[i]<<endl;


return 0;
  //techindetail.com
}Code language: C++ (cpp)

Gaussian Elimination Method C++ Program

Gaussian elimination is a powerful numerical method used to solve systems of linear equations.

By utilizing the Gaussian elimination algorithm, the program allows users to input a system of linear equations, and it quickly solves for the unknown variables, providing accurate solutions in a fraction of the time

With its speed and accuracy, this program is an indispensable tool for anyone dealing with linear algebra and numerical analysis.

Must Read: Gauss Jordan Method C++

Example

Find the Solution of the following Linear Equations using the Gauss Elimination Method.

x + y + z = 6
x – y + z = 2
2x – y + 3z = 9

Sol:  In this method, the variables are eliminated and the system is reduced to the upper triangular matrix from which the unknowns are found by back substitution.

Related:

Bisection Method C++ Solved Example

Regula Falsi Method C++ Solved Example

Step 1: Write the given System of Equations in the form of AX = b, i.e. Matrix Form.

Where as,
A = Coefficient Matrix,
X = variables (Column Matrix),
b = constants (Column Matrix.

Step 2: Find Augmented Matrix C = [ Ab ]

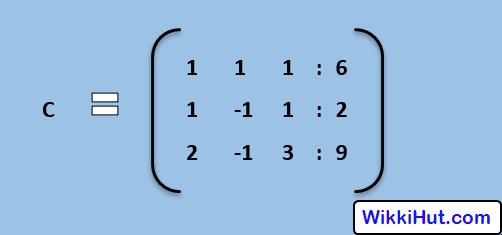
Step 3: Transform Augmented Matrix into Upper Triangular Matrix.

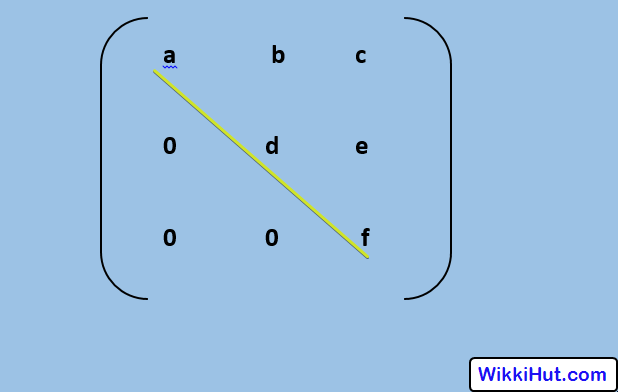
In the upper Triangular matrix, all the elements below the Diagonal are zero

Note: Only Row operations are allowed.

Now as you can see that it is now reduced to an upper triangular matrix.

Step 4:  Find equations corresponding to upper triangular matrix.

Now by using back Substitution reconstruct the equations and find the corresponding values of the variables x, y, and z.

1.x + 1.y + 1.z = 6
0.x – 2y + 0.z = – 4
0.x – 0.y + 2z = 6

Therefore,

x + y + z = 6
-2y = -4
2z = 6

Now, Put the value of y and z into eq. 1.
X + 2 + 3 = 6 –> x = 1
Therefore, the roots of the three equations are x = 1 , y = 2, z= 3

Suggestion: Gauss Elimination With Partial Pivoting C++