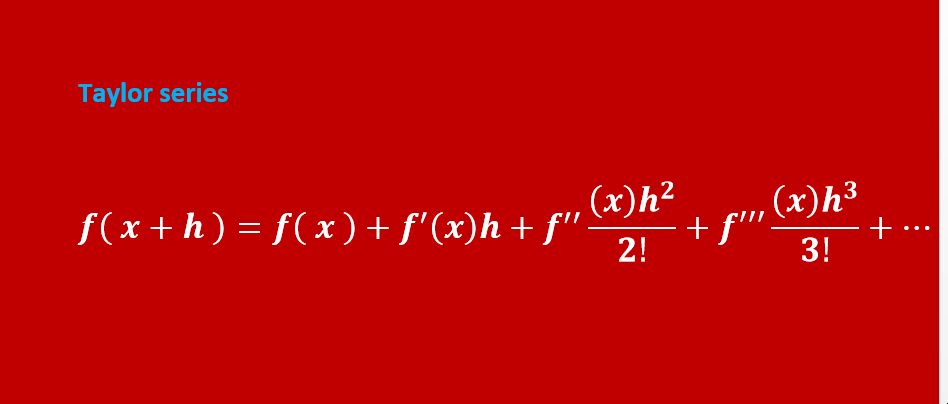
What is Taylor Series
In mathematics, sometimes it is really difficult to evaluate some functions. In such cases, we use the approximation formulas where the function is expressed as a series. There are two such approximation formulas:
- Taylor series formula
- Maclaurin series formula
Taylor series formula helps us in writing a function as a series (or sum) of terms involving the derivatives of the function.
This formula helps us in finding the approximate value of the function.
Taylor series formula
f( x+h )=f( x ) + f'(x)h + f”{(x) h2}/2! + f”'{(x) h3}/3! + ⋯
or
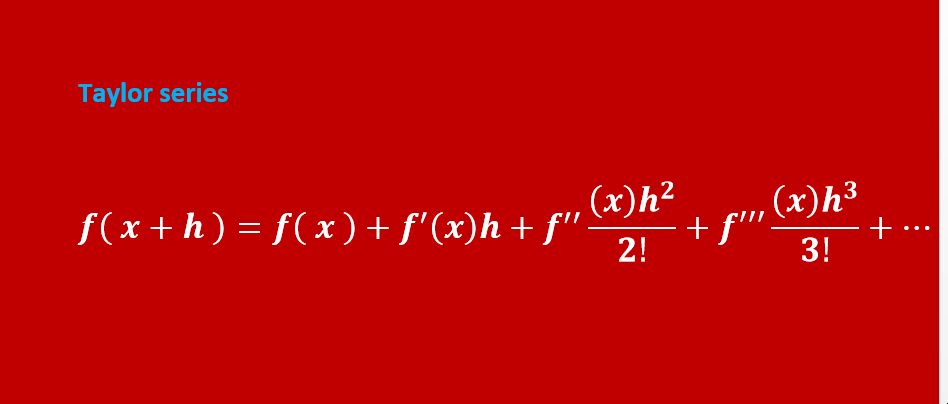
You can try a Taylor series calculator to find the Taylor expansion of the given function according to the above formula.
1 Example Solved
Given f(4)=125, f’(4)=74, f’’(4)=30, f’’’(4)=6. Find f(6)=?
Sol: Here h = 2, and all other derivates are zero.
F(6) = 125 + 74(2) + 30(2)2 / 2 + 6(2)3 / 3 + 0 + 0 + 0
F(6) = 125 + 148 + 60 + 8
F(6) = 341 Ans.
2 Example Solved
Given The Ordinary differential dy/dx = 3×2 – x2y, y(2)=5. Find 2nd Order Polynomial for y as a function of x & x=2.
Sol.
Let the 2nd order polynomial be a0+a1x + a2x2
Using taylor series, f( x+h )=f( x ) + f'(x)h + f”{(x) h2}/2! + f”'{(x) h3}/3! + ⋯
Given, y(2) = 5 and x =2.
Therefore,
y’(2) = 3x2 – x2y
3(2)2 – (2)2y
12 – 4y
Y = 12/4
Y=3, put this value of y
Y’(2)=3(2)2 – (2)-8
Y’(2) = -8
Now, y’’(2) = (d/dx)(3x2 – x2y)
6x – (d/dx)(x2y)
Use product Rule of differentiation, xy
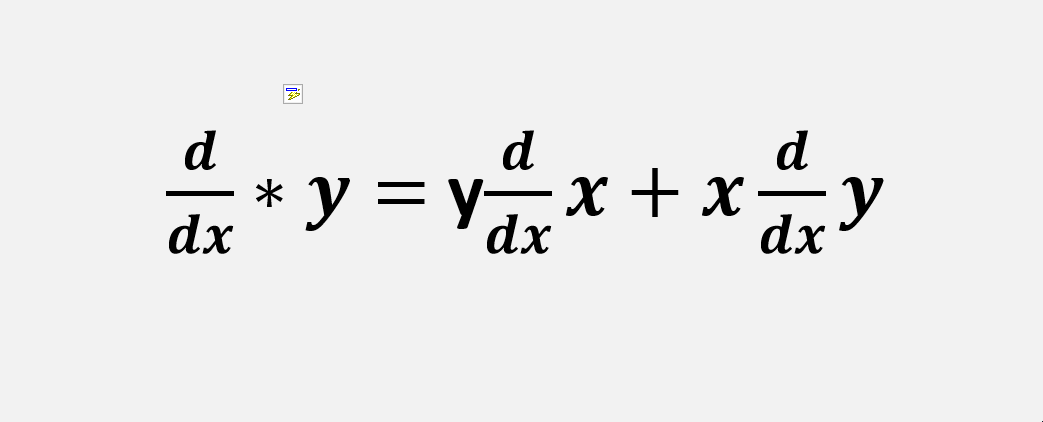
6x – ( 2xy – x2 d/dx(y))
6(2) – 2(2)(5) – 22(-8) = 24
Therefore, y(2+h)= 5 + (-8)h + 24h2
Y(2+h) = 5 – 8h + 12h2
Y(x) = 5-8(x-2)+12(x-2)2
Y(x)=12x2-56x+69 (Answer.)
Suggested Methods:
