
Got data that doesn’t make a straight line? No worries! Polynomial regression helps find the right curve for your numbers.
Let’s learn how to use it for fitting a second-order curve to your data – perfect for spotting trends in a snap.
Polynomial Regression Example
Let’s say you have the following data points:
| x | 1.0 | 2.0 | 3.0 | 4.0 |
| y | 6.0 | 11.0 | 18.0 | 27.0 |
Solution:
Let Y = a1 + a2x + a3x2 ( 2nd order polynomial ).
Here, m = 3 ( because to fit a curve we need at least 3 points ).
Since the order of the polynomial is 2, therefore we will have 3 simultaneous equations as below.
1. Polynomial Regression Formula
To learn more, see what is Polynomial Regression
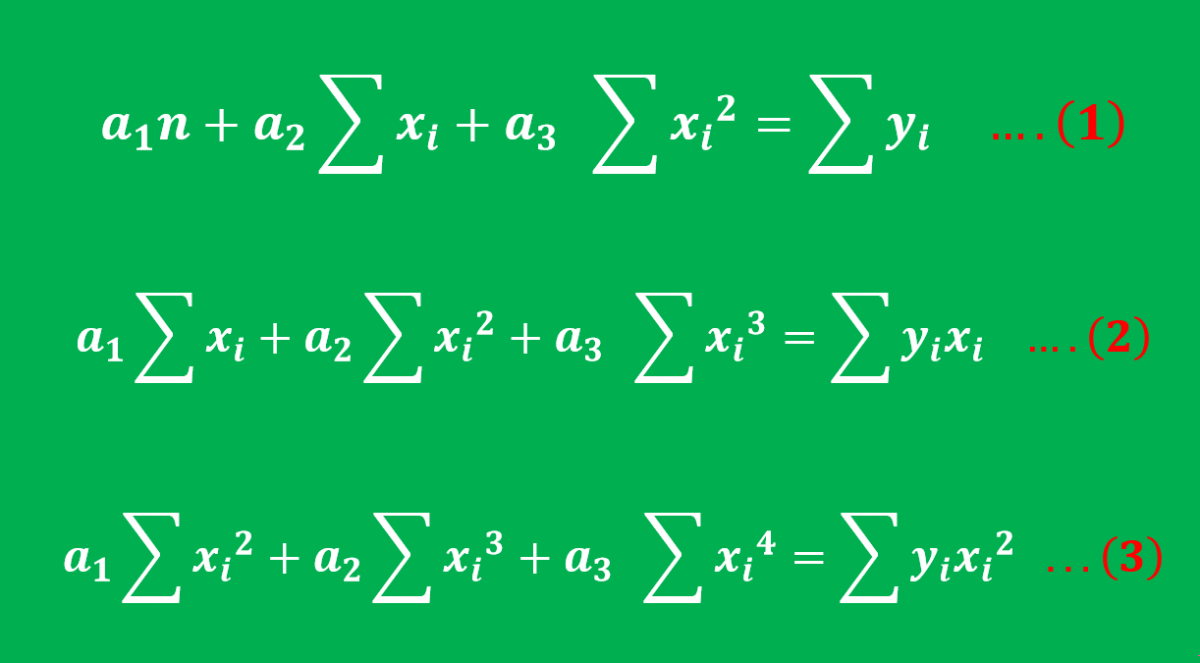
2. Evaluate Formula
Now we have to evaluate the values that are required according to the above equations.
Let us find the value of x2, x3, x4, yx, and yx2.
| x | y | x2 | x3 | x4 | yx | yx2 |
|---|---|---|---|---|---|---|
| 1.0 | 6.0 | 1 | 1 | 1 | 6 | 6 |
| 2.0 | 11.0 | 4 | 9 | 16 | 22 | 44 |
| 3.0 | 18.0 | 9 | 16 | 81 | 54 | 162 |
| 4.0 | 27.0 | 16 | 36 | 256 | 108 | 432 |
| ∑xi=10 | ∑yi=62 | ∑x2=364 | ∑x3=524 | ∑x4=354 | ∑yx=190 | ∑yx2=644 |
3. Substitute Values
Put the values in the above 3 equations as below.
4a1 + 10a2 + 30a3 = 62 …. ( 1 )
10a1 + 30a2 + 100a3 = 190 …. ( 2 )
30a1 + 100a2 + 354a3 = 644 … ( 3 )
4. Make Matrix
In order to solve the above 3 simultaneous equations, we will write the above equations in the form of matrices as below.
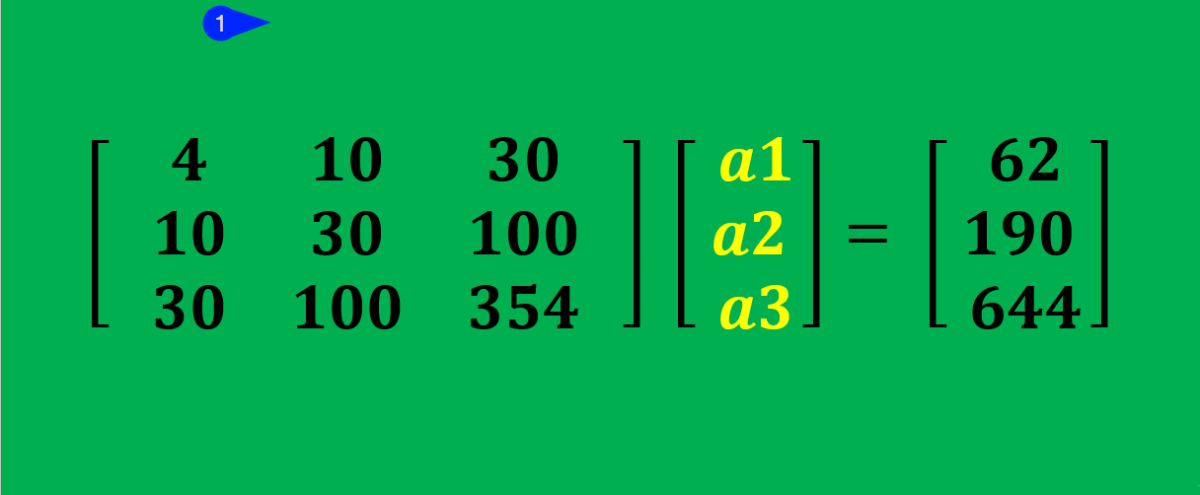

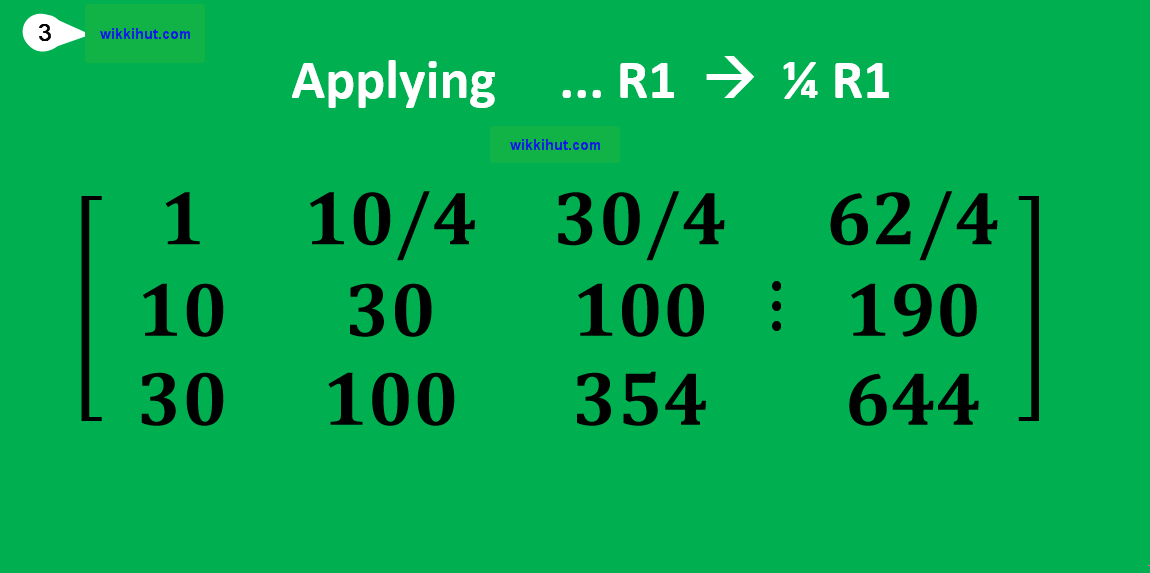
5. Use Matrix Elimination
By using matrix elimination techniques, you can solve for the coefficients a, b, and c.



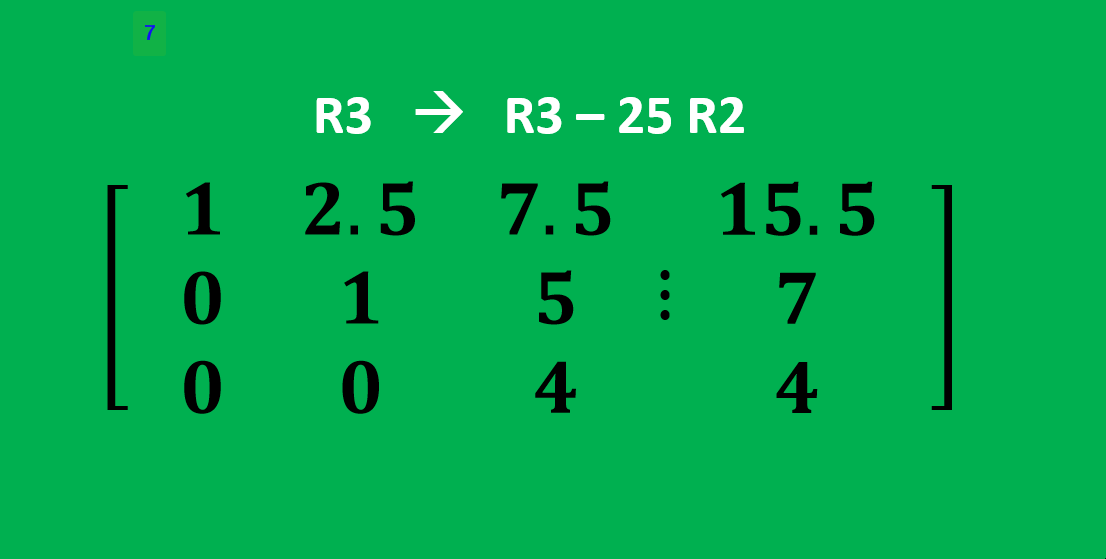
Now by using back substitution, we can find the values of a1, a2, and a3.
Here, 4a3 = 4 , a3 = 1
And, a2 + 5a3 = 7 , a2 = 2
Also, a1 + 2.5a2 + 7.5a3 = 15.5 , a1 = 3
Therefore, a1 = 3, a2 = 2, a3 = 1.
6. Final Equation
The Quadratic equation becomes: Y = 3 + 2x + x2, or
Sol:- Y = x2 + 2x + 3
This is your second-order polynomial regression equation that closely matches your given data points!
Suggestion:
- Newtons Interpolation
- Lagrange’s Interpolation
- Bisection method
- Regula falsi method
- Linear Regression
Conclusion
In simple words, polynomial regression helps us find the right curve that fits our data points, even when they don’t play nicely with a straight line.
It’s a bit of math magic that lets us make predictions and understand trends in our data.
Just remember, not every problem needs a fancy high-degree polynomial – sometimes, a simple line works best.
