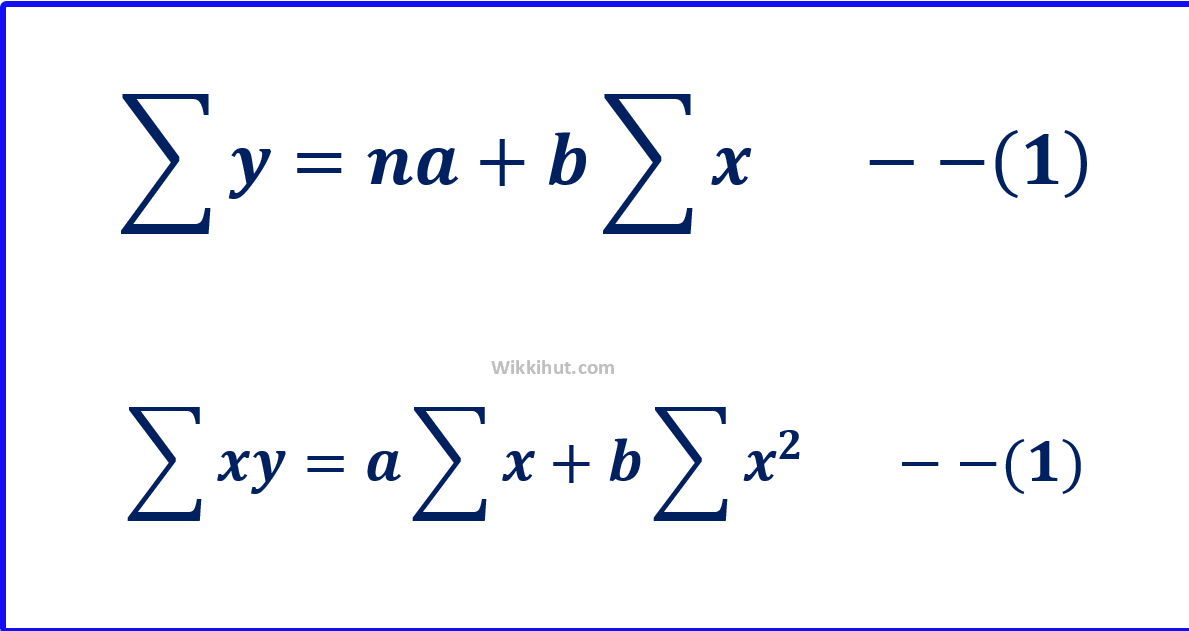
Ad
Linear Regression
| x | 1 | 3 | 4 | 6 | 8 | 9 | 11 | 14 |
| y | 1 | 2 | 4 | 4 | 5 | 7 | 8 | 9 |
From the given data find the regression line of y on x. Estimate value of y when x = 10.
Find function y = f (x)
Y = f(x) = a + bx ( equation of line y = mx+c )
Ad
Y = f(x) = a + bx, is the line of regression of y on x
When a & b are given by the following equations
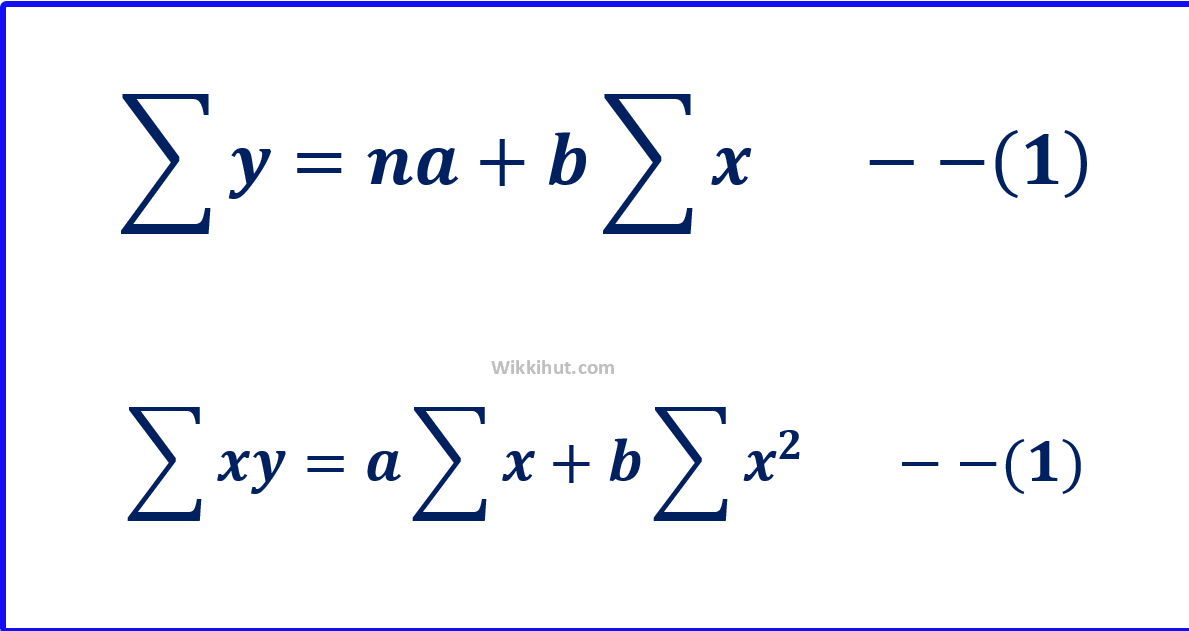
Where as;
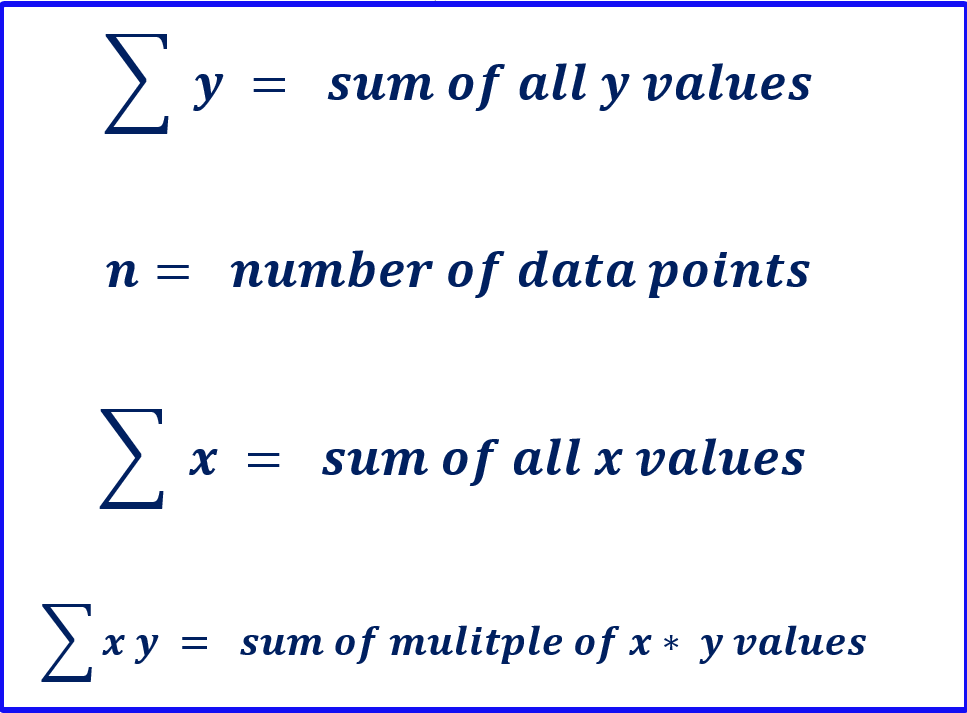
Now you have to calculate the values which are going to be required in the above equations such as;
- sum of all x values
- sum of all y values
- sum of product of x and y
| x | y | xy | x2 |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 3 | 2 | 6 | 9 |
| 4 | 4 | 16 | 16 |
| 6 | 4 | 24 | 36 |
| 8 | 5 | 40 | 64 |
| 9 | 7 | 63 | 81 |
| 11 | 8 | 88 | 121 |
| 14 | 9 | 126 | 196 |
| ∑x=56 | ∑y=40 | ∑xy=364 | ∑x2=524 |
Now put these values in the equation 1 and 2, we get
8a + 56b = 40, ( eq. 1 )
56a + 542b = 360 ( eq. 2 )
Now, you need to find the value of a and b in these two equations by simplifying them.
Ad
We get, a = 6/11 and b = 7/11
Therefore the equation becomes y = 6/11 + (7/11)x
Suggestion:
