
In this article, we will learn about the derivatives of 1/x^2 or 1/x2, Different ways to find its derivative, and other important concepts related to its derivative.
The derivative of 1/x^2 is −2x−3 or -2/x3.
What is a derivative?
A derivative in mathematics is defined as the “Rate of change in the value of a function with respect to the change in the independent variable”.
For example, if f(x) is a function, its derivative written as f‘ (x) or f1(x) measures how the output value of f(x) changes when the input value x is changed.
Differentiation is a mathematical tool that helps to find the derivative of a function.
The function 1/x2,
The function 1/x2 is a mathematical expression that cannot have the value of x = 0 because dividing by zero is undefined in mathematics. One of the important properties of this function is that as we increase the value of x, the value of the function moves close to zero. When the value of x tends to infinity the value of the function tends to zero.
Derivative using the First Principle:
The First Principle of derivatives is a mathematical method of finding the derivative of a function, it uses the concept of Limits to find the derivative of a function.
If f(x) is a function the derivative of f(x) using the first Principle is expressed as:
f’(x) = f (x + h) – f(x) / h where h is a difference between the point at which we want to find the derivative.
Now let us find the derivative of1/x2 using first principle.
Step 1: f(x)=1/x2
Step 2: The expression for the derivative of a function using first principle is
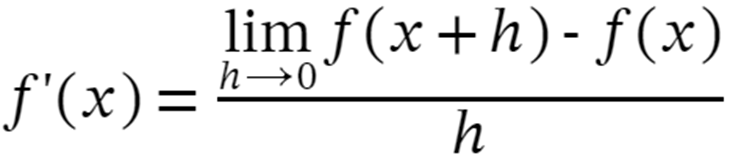
Step 3: Replace the function with our function f(x)=1/x2 in the above expression
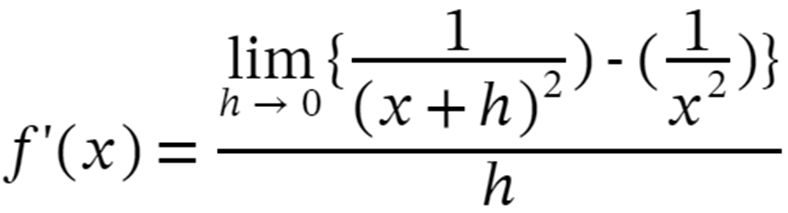
Step 4: Solve the expression as:
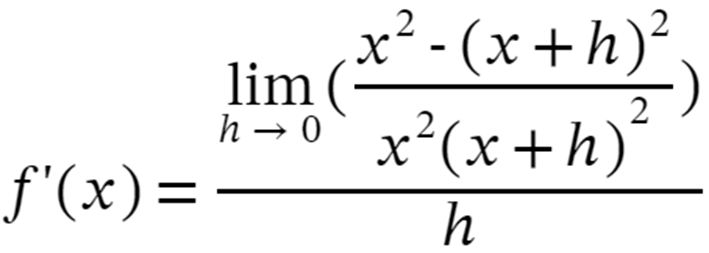
Step 5: Expand and cancel out the like terms we get:
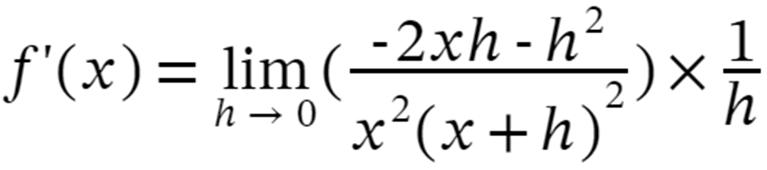
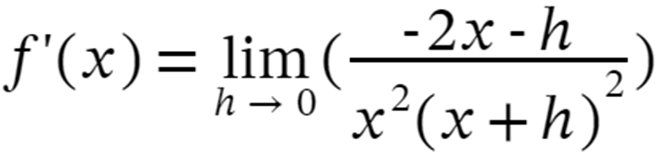
Step 6: Now apply the limits i.e. h–>0 we get,
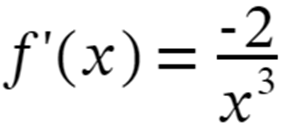
So, the derivative of f(x) = 1/x2 is f'(x) = -2/x3
Direct Method (power method):
In this method we calculate the derivative of a function by multiplying the power and reducing the power by 1.
For example if f(x) = xn is a function its derivative is f'(x) = nxn-1.
This is the simplest method to calculate the derivative of a function
Now let us calculate the derivative of our function f(x) = 1/x2 using Direct method.
f(x) = 1/x2
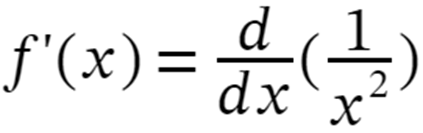
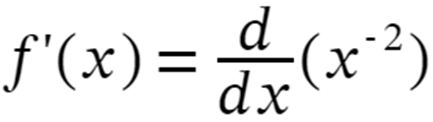
f'(x) = -2(x-2-1 )
f'(x) = -2/x-3
Using direct method we find the derivative of the function which is same as we find through the first principle, but the direct method (Power rule) is much shorter than the First Principle.
Also Read: Taylor series Sinx
