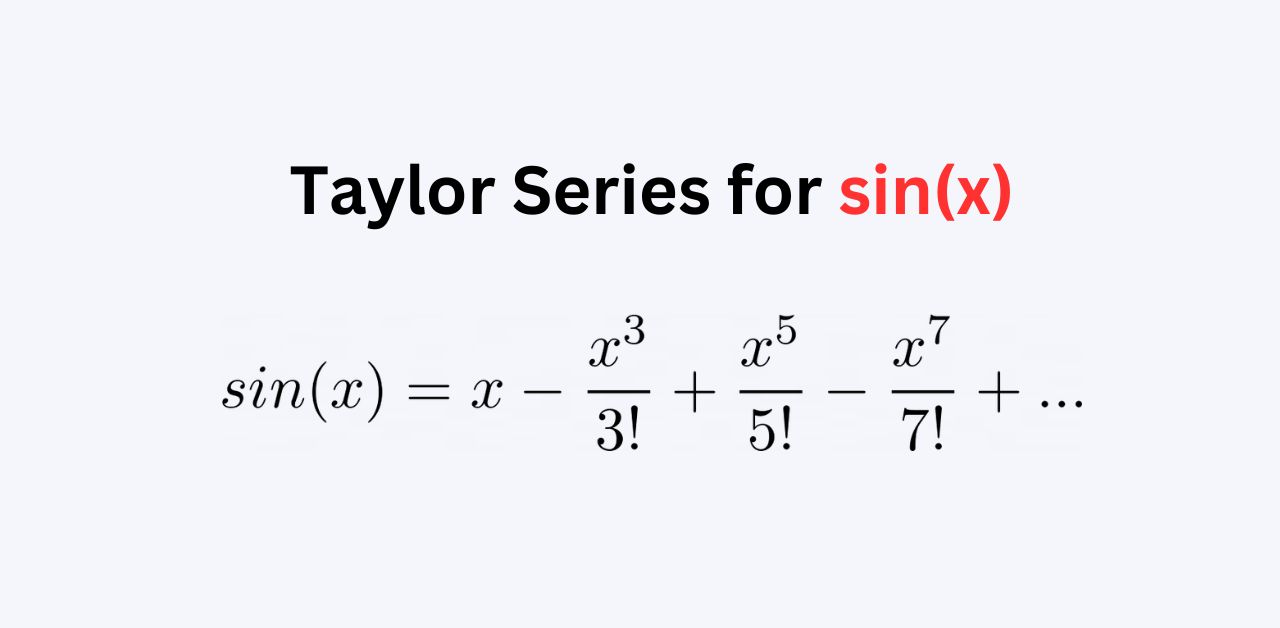
The expansion of Taylor series for SinX is as follows:
sin(x) = x – (x³ / 3!) + (x⁵ / 5!) – (x⁷ / 7!) + …
This infinite series continues, with each term involving an increasing power of x and alternating signs.
The factorial (n!) in the denominator accounts for the coefficients, ensuring the correct progression of terms.
Taylor Series Intro:
The Taylor series is a mathematical representation of a function as an infinite sum of terms.
It enables us to approximate the behavior of a function around a specific point using its derivatives.
The Taylor series for sin(x) is particularly intriguing as it allows us to approximate the values of the sine function for any given angle.
For more details see What is Taylor Series.
Taylor Series sin(x):
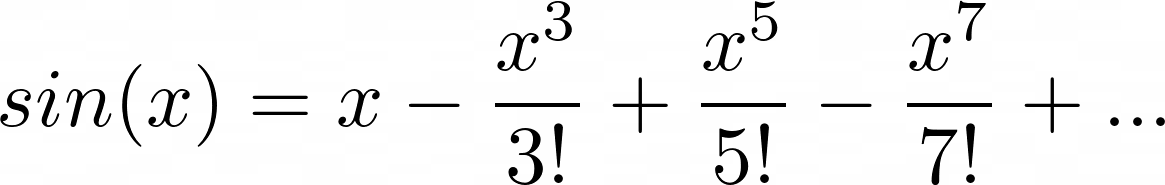
Let’s examine how the Taylor series for sin(x) can be utilized to approximate the sine function.
Example 1: Approximating sin(x) using the first three terms.
To approximate sin(x) using the Taylor series, we can truncate the series to a finite number of terms.
When x = π/4:
Let’s consider the first three terms and approximate sin(x) when x = π/4.
Since sin(x) = x – (x³ / 3!) + (x⁵ / 5!) ,
∴ sin(π/4) = (π/4) – ((π/4)³ / 3!) + ((π/4)⁵ / 5!)
Calculating the values:
sin(π/4) = 0.7854 – 0.0668 + 0.0041 ≈ 0.7227
The actual value of sin(π/4) is approximately 0.7071, so our approximation using three terms is reasonably close.
Example 2: Increasing accuracy with more terms.
To achieve a more accurate approximation, we can include more terms in the Taylor series expansion.
When x = π/3:
Let’s consider the first five terms to approximate sin(x) at x = π/3.
Since sin(x) = x – (x³ / 3!) + (x⁵ / 5!) – (x⁷ / 7!) + (x⁹ / 9!)
∴ sin(π/3) = (π/3) – ((π/3)³ / 3!) + ((π/3)⁵ / 5!) – ((π/3)⁷ / 7!) + ((π/3)⁹ / 9!)
Calculating the values:
sin(π/3) = 1.0472 – 0.1443 + 0.0111 – 0.0004 + 0.0000 ≈ 0.8660
The actual value of sin(π/3) is approximately 0.8660. With five terms, our approximation is extremely close to the true value.
When x = 0,
The formula for the Taylor series of sin(x) for x = 0, simplifies as follows:
sin(0) = 0 – (0³ / 3!) + (0⁵ / 5!) – (0⁷ / 7!) + …
Since any term with x = 0 will evaluate to 0, the formula reduces to:
∴ sin(0) = 0
Therefore, when x = 0, the value of sin(x) is also 0.
Conclusion:
The Taylor series for sin(x) is a powerful mathematical tool that enables us to approximate the sine function with increasing precision.
By utilizing a finite number of terms from the series, we can obtain accurate approximations for a wide range of angles.
