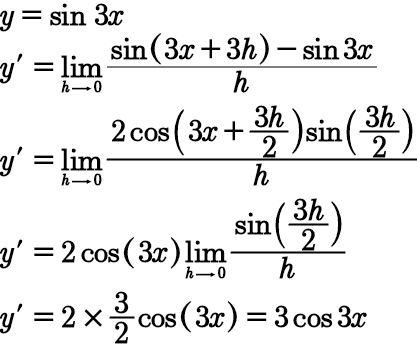
In this Article we will understand the formula of a sine function sin(3x), the formula of sin3x is as follows:
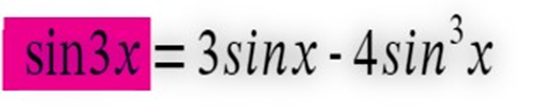
Sin(3x) = 3sinx – 4sin3x
Now we will understand every concept of trigonomatry related to this function one by one, like how it is derived, what are its properties etc.
What is a Trigonometric function:
Trigonometry explains the relation between angles and the corresponding sides of triangles
Trigonometric functions, on the other hand defines these relationships as ratios.
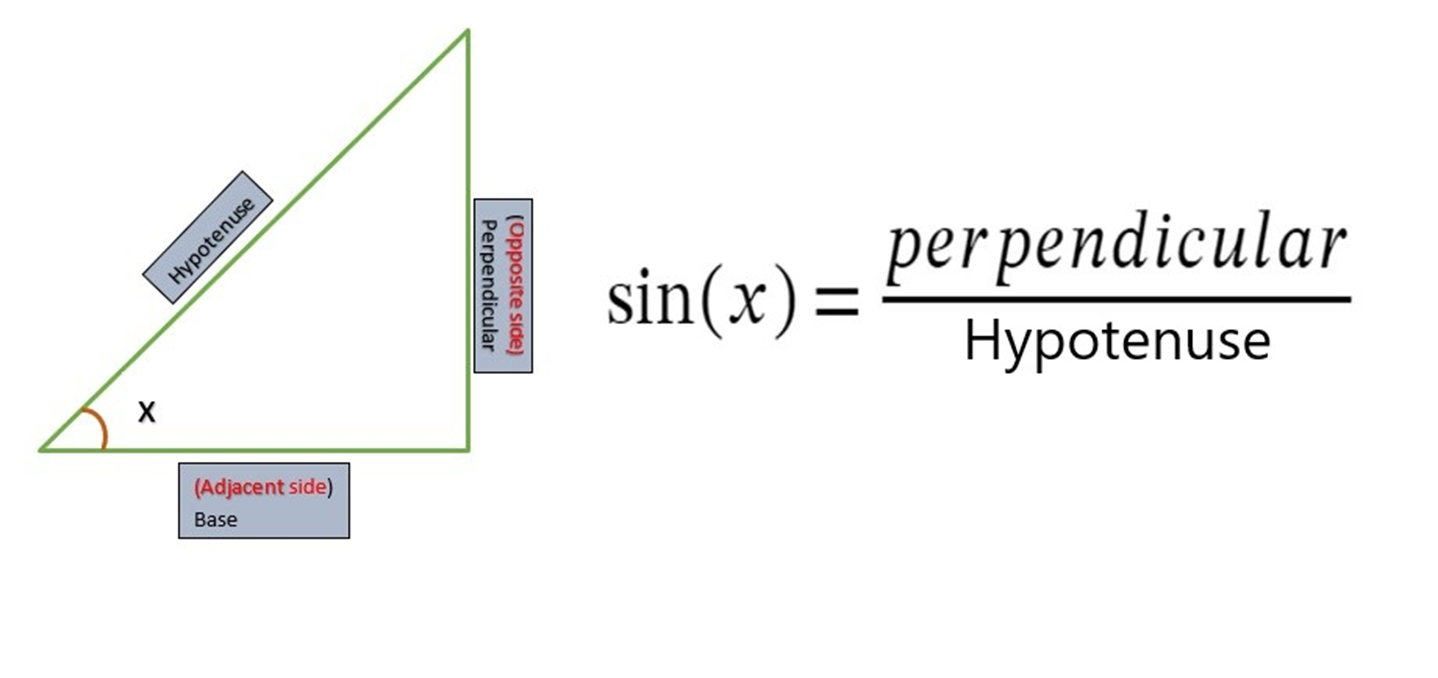
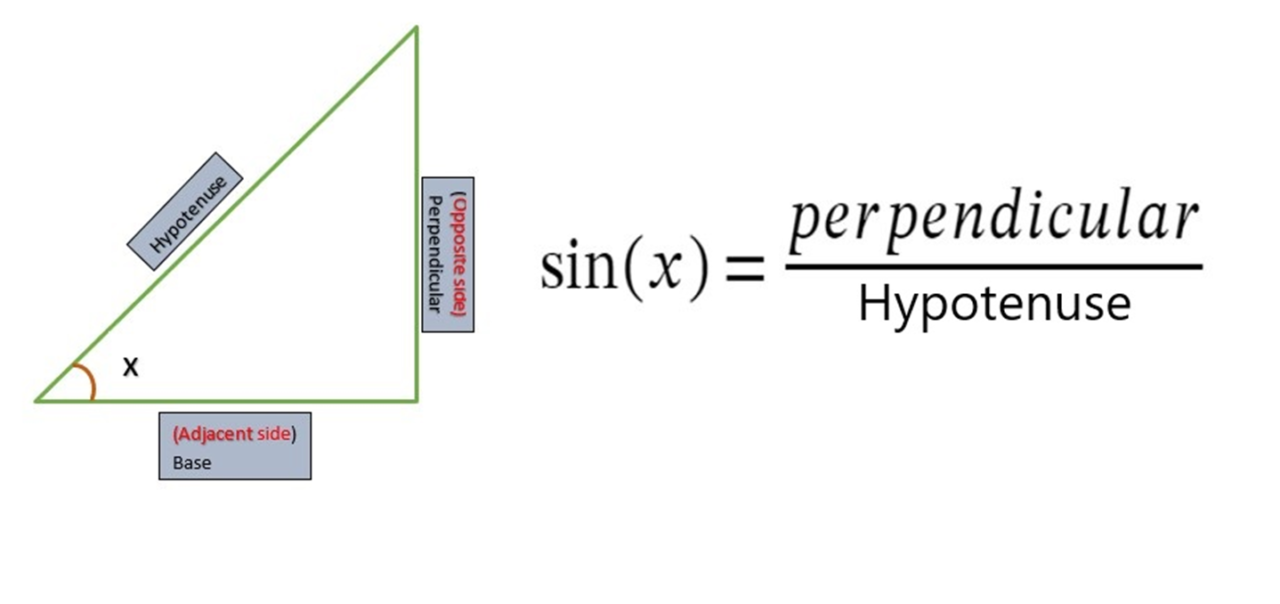
Trigonometric Function Sin(x):
The Sine function, written as sin(x), is a trigonometric function that maps an angle to the ratio of the length of the side opposite the angle to the hypotenuse of a right triangle. The value of sine function oscillates between (-1,1).
Some Trigonometric identities:
- Double Angle Formula for Sine:
sin(2x) = 2sin(x)cos(x) - Sum-to-Product Formula for Sine:
sin( A + B ) = sin( A ) cos(B) + cos(A)sin(B) - Double Angle Formula for cosine:
cos( 2x) = 1- 2sin2(x)
Derivation of sin(3x) Formula:
Step 1: we need to rewrite the sin(3x) as:
sin( 3x ) = sin ( 2x + x )
Step 2: Here we use the Sum-to-product Formula of sine as:
sin( 3x ) = sin( 2x )cos( x ) + cos( 2x )sin( x )
Step 3: we already know the double-angle Formula of sine and cosine, so we replace the sin(2x) and cos(2x) with their respective values as:
sin ( 3x ) = {2sin( x )cos( x )}cos( x ) + {1 – 2sin2( x )}sin( x )
Step 4: Simplify the equation by multiplying the terms
sin ( 3x ) = 2sin( x )cos2( x ) + sin( x ) – 2sin3( x )
Step 5: Use the value of cos2(x) as (1-sin2(x))
sin( 3x ) = 2sin( x ){1 – sin2( x )} + sin( x ) – 2sin3( x )
Step 6: Simplify and combine the like terms:
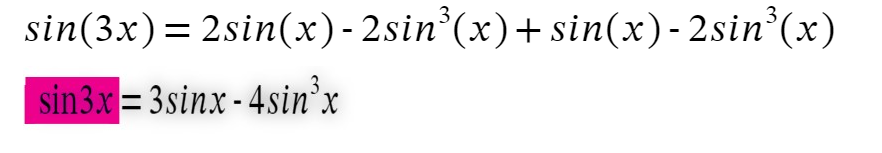
Example:
Q: Find the value of sin(3π/4)
To find sin(3π/4), we can use the derived formula for sin(3x):
sin(3x) = 3 sin(x) – 4sin3(x)
In this case, x is π/4. So, we can substitute π/4 into the formula:
sin(3π/4) = 3 sin(π/4) – 4sin3(π/4)
Now we know that: sin(π/4) = √ (2)/2
Substitute the value of sin(π/4) in the above equation we get:
sin(3π/4) = √ (2)
Derivative of Sin(3x):
To find the derivative of sin(3x) we will first use the direct method as:
f(x) = sin(3x)
f'(x) = d /dx (sin(3x))
f'(x) = cos(3x)*d/dx(3x)
f'(x) = cos(3x)*3
f'(x) = 3cos(3x)
Derivative of sin(3x) using first principle:
The expression for calculating derivative using first principle is as
f'(x) = limt { f(x+h) – f(x) }/ h