
Breadth First Search (BFS)
Breadth First Search (BFS) or breadth first traversal algorithm traverses a Graph in a breadth-wise manner and stores the visited nodes in a queue.
BFS traversal algorithm uses a queue to store the nodes of each level when they are visited, and then these nodes are visited one by one after that the adjacent nodes are visited. The terminating condition is when the queue is empty.
In BFS traversal one node is selected as a starting position. This selected node is visited and saved in a queue. Then all the unvisited adjacent nodes are visited and stored in the queue.
Finally, the adjacent nodes to these nodes are visited and saved in the queue, until the entire graph has been traversed.
BFS Algorithm
- Select one node, visit it and save it in a queue.
- Traverse the adjacent nodes of starting node and save these.
- Visit the adjacent unvisited vertices and save in the queue.
- If no adjacent vertex is found, remove the first vertex from the queue.
- Traverse until the queue is empty.
BFS Example 1
Now look at the breadth first traversal of this graph.
Let us start with vertex 1. Its adjacent vertices are 2, 8, 3. Now pick one by one these vertices say vertex 2.
The unvisited vertices to vertex2 are 4, 5. Visit both these, and go back to the unvisited nodes of 1 and pick another one.
Pick vertex 3, the unvisited adjacent vertices to 3 are 6 and 7. Now there remain no unvisited nodes of vertex 8, 4, 5, 6, and 7.
Therefore, the sequence is 1, 2, 8, 3, 4, 5, 6, and 7. We need a queue to store these values and add unvisited vertices adjacent to the one just visited at the rear and read at from to the find the next vertex to visit.
BFS Example 2
Let us take an example.
Breadth first traversal of the graph above is 1, 2, 3, 4, 5, 6, 7, 8. Also the sequence 1, 3, 2, 6, 5, 4, 7, 8 is valid. The queue stores all the visited nodes at each level.
BFS Flowchart
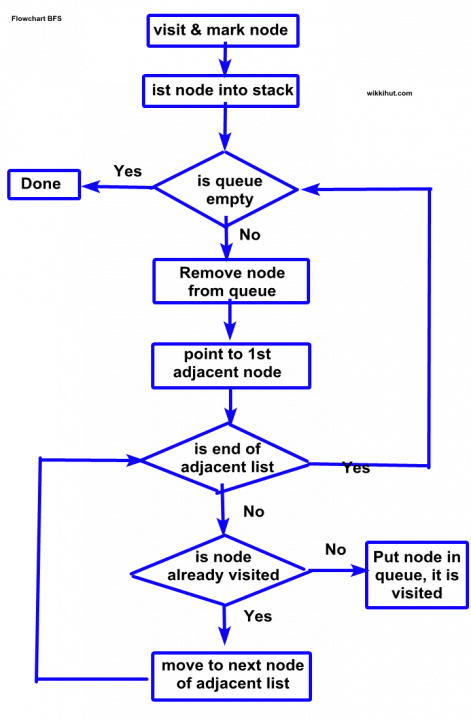
See Also: Depth First Search (DFS)
